WIENER NORBERT (1894-1964)… Dire que Wiener est le père de la cybernétique ou qu’il est le « philosophe de l’automation » signifie qu’il a élaboré, dans le cadre initial de la théorie de la communication, des méthodes mathématiques qui ont permis de traiter de manière semblable de vastes classes d’objets.
Table des matières
SOMMAIRE
- Introduction
- Éléments biographiques
- Le mouvement brownien
- L’analyse harmonique généralisée
- Théorèmes taubériens
- La transformée de Fourier complexe
- La cybernétique
- Bibliographie
- Classification
- Autres références
WIENER NORBERT (1894-1964)
En Wiener, il ne faut pas voir que le savant ; il est important de souligner la qualité exceptionnelle de l’homme dans ses déclarations et son comportement : si Wiener a travaillé avec l’armée pendant la Seconde Guerre mondiale, il est, à l’encontre de beaucoup d’autres scientifiques, resté très lucide devant les dangers d’une telle collaboration qu’il a dénoncés en des termes violents.
Éléments biographiques
Norbert Wiener est né à Columbia (Missouri) le 26 novembre 1894. Enfant prodige, il étudie les mathématiques en même temps que la philosophie et la biologie et soutient, à dix-huit ans, une thèse de logique mathématique à l’université Harvard.
Lors d’un voyage en Europe avec sa famille, en 1913-1914, il est à Cambridge l’élève de Russell qui aura sur lui une grande influence.
De retour aux États-Unis, il est nommé, en 1919, professeur au Massachusetts Institute of Technology (M.I.T.) où il enseignera jusqu’en 1960. Il meurt à Stockholm le 18 mars 1964.
Wiener a écrit sa biographie dans deux ouvrages dont les titres sont d’une ironie un peu grinçante : Ex-Prodigy : My Childhood and Youth et I Am a Mathematician. The Later Life of a Prodigy.
Le mouvement brownien
Le mouvement brownien est un des exemples les plus célèbres de processus aléatoire (cf. processus stochastiques). Vers 1905, Einstein et M. von Smoluchowski avaient étudié, indépendamment l’un de l’autre, le comportement des particules agitées par le mouvement décrit pour la première fois par le botaniste anglais Robert Brown en 1828.
Les recherches de Wiener sur ce sujet vont motiver toute son œuvre mathématique ultérieure : son idée initiale est d’étudier l’ensemble des chemins des particules en tant qu’espace fonctionnel. Citons J. L. Doob : « Dans une série d’articles à partir de 1920, Wiener a entrepris une analyse mathématique du mouvement brownien. Il était admis que les trajectoires browniennes étaient régies par des lois probabilistes et il semblait plausible que ces trajectoires étaient continues.
Le problème était de construire et d’analyser un modèle mathématique rigoureux. Plus d’une décennie avant la formalisation de la probabilité par Kolmogorov, Wiener a construit un modèle mathématique du mouvement brownien dont les probabilités de base étaient les valeurs d’une mesure définie sur des sous-ensembles d’un espace de fonctions continues. Depuis lors, cette mesure est appelée couramment « mesure de Wiener. »
Wiener construit la théorie mathématique correspondante d’intégration dans un espace fonctionnel dans son article Differential-Space publié en 1923.
Il établit que « presque sûrement » (au sens de la probabilité) le chemin d’une particule est une courbe non dérivable, ce qui avait été pressenti par Jean Perrin dans son livre Les Atomes à partir de la remarque que la particule n’a aucune direction déterminée a priori en chaque point.
Une quinzaine d’années plus tard, dans son article The Homogeneous Chaos, Wiener reprendra l’étude d’une classe de processus englobant le mouvement brownien, mais avec cette fois les outils de la théorie ergodique qu’il perfectionne à cette occasion.
L’analyse harmonique généralisée
Les processus étudiés par Wiener, comme le mouvement brownien, les bruits ou les rayons lumineux, n’étaient pas redevables de l’analyse harmonique classique.
Il écrivait : « Les deux théories de l’analyse harmonique contenues dans le développement classique en série de Fourier et la théorie de Plancherel n’épuisent pas les possibilités de l’analyse harmonique.
Les séries de Fourier ne s’appliquent qu’au cas très particulier des fonctions périodiques, tandis que la théorie de Plancherel ne s’applique qu’aux fonctions de carré sommable, et donc qui tendent vers zéro en moyenne quand la variable tend vers l’infini. Aucune de ces deux théories n’est utilisable pour étudier un rayon de lumière blanche supposé de durée infinie. »
Dans l’important mémoire Generalized Harmonic Analysis de 1930, Wiener construit une théorie mathématique qui puisse répondre aux besoins des physiciens. Il étudie l’espace S des fonctions complexes f mesurables sur R pour lesquelles la fonction de covariance :

est définie en tout point x ∈ R ; les fonctions presque périodiques de Bohr et les réalisations de nombreux processus stochastiques sont de ce type.
Wiener établit que, pour f appartenant à S, la fonction de covariance est une transformée de Fourier-Stieltjes :

égalité vraie pour presque tout x, où la fonction croissante bornée S, unique après normalisation, est la distribution spectrale de f.
Poursuivant le parallèle avec la théorie classique, Wiener définit, pour f ∈ S, l’analogue s de sa transformée de Fourier, par une formule trop technique pour être donnée ici. Un des résultats principaux pour les applications est la formule :

qui exprime que la « variation quadratique » de s est égale à la « moyenne du carré du module » de f. La formule de réciprocité est délicate et demande une extension de la notion d’intégrale.
Wiener a ensuite étendu ces résultats à plusieurs variables et a donné des applications aux fonctions presque périodiques.
Théorèmes taubériens
L’article sur l’analyse harmonique généralisée faisait appel à des techniques fines d’analyse que Wiener développe sous une forme systématique dans son article Tauberian Theorems de 1932.
Il s’agit d’un vaste ensemble de théorèmes unifiés par l’utilisation de la convolution et de la transformation de Fourier (classique) ; la terminologie provient du théorème de Tauber (1897), le premier de ce type, qui s’énonce ainsi : Si une série de terme général an est telle que Σanxn tende vers S pour x tendant vers 1 à gauche, alors Σan = S.
Les théorèmes taubériens de Wiener sont de plusieurs formes ; un des résultats essentiels est le suivant.
Théorème. Soit K1 une fonction intégrable sur R dont la transformée de Fourier ne s’annule en aucun point de R. Soit h une fonction mesurable bornée sur R. Alors, si l’on a :

on a aussi :

pour toute fonction intégrable K ; ici f * g désigne le produit de convolution sur R défini par

Ce type de théorème permet d’obtenir une nouvelle démonstration du théorème sur la distribution des nombres premiers.
Les théorèmes taubériens de Wiener font jouer un rôle essentiel aux zéros des transformées de Fourier et sont liés au problème de la synthèse harmonique (cf. analyse harmonique, chap. 2). Un des théorèmes fondamentaux obtenus par Wiener à ce propos est le suivant.
Théorème. Soit Σ un ensemble de fonctions intégrables sur R. Une condition nécessaire et suffisante pour que les combinaisons linéaires finies de translatées de fonctions de Σ soient denses dans L1(R) est que les transformées de Fourier des fonctions de Σ n’aient aucun zéro commun.
Ce type de résultat posait implicitement le célèbre « problème de Wiener » : Soit f et g deux fonctions intégrables sur R ; est-il vrai que g est limite dans L1 de combinaisons linéaires finies de translatées de f dès que sa transformée de Fourier s’annule sur l’ensemble des zéros de la transformée de Fourier de f ? La réponse est négative comme l’a montré P. Malliavin en 1959.
Enfin, on peut voir le point de départ de la théorie des […]
La transformée de Fourier complexe
En 1932-1933, Wiener travaille en collaboration avec le mathématicien anglais R. Paley ; ce dernier mourra accidentellement avant la publication en 1934 de leur ouvrage commun Fourier Transforms in the Complex Domain.
Le résultat le plus célèbre de ce livre est le théorème de Paley-Wiener qui caractérise les transformées de Fourier complexes des fonctions de carré sommable nulles en dehors d’un intervalle [− A, + A] comme les fonctions entières de type exponentiel ≤ A.
Ce théorème a d’innombrables applications en mathématiques pures et dans la théorie de la prédiction non linéaire.
La cybernétique
Pendant la Seconde Guerre mondiale, Wiener participe à l’élaboration de méthodes de défense antiaérienne et est amené à réfléchir sur leurs deux aspects principaux : la transmission des messages, c’est-à-dire le problème de la communication, et le couplage de l’homme et de la machine.
Dans son célèbre mémoire Extrapolation, Interpolation and Smoothing of Stationnary Time Series, Wiener développe la théorie des systèmes linéaires optimums qui contient le problème de la prédiction linéaire et celui du filtrage. Il publiera en 1958 ses résultats sur la prédiction non linéaire dans son livre Nonlinear Problems in Random Theory.
Les méthodes aléatoires de Wiener s’appliquaient à une vaste classe de problèmes et permettaient d’aborder du même point de vue des objets aussi variés que la théorie de la communication, le comportement des servomécanismes et des ordinateurs, le système nerveux.
A lire aussi
- Shannon- Wiener – Weaver : modèle de la communication
- Modèle de la communication de Shannon- Wiener – Weaver
- Théorie de la communication et approche systémique
- Médiologie ou théorie des médiations techniques et institutionnelles de la culture
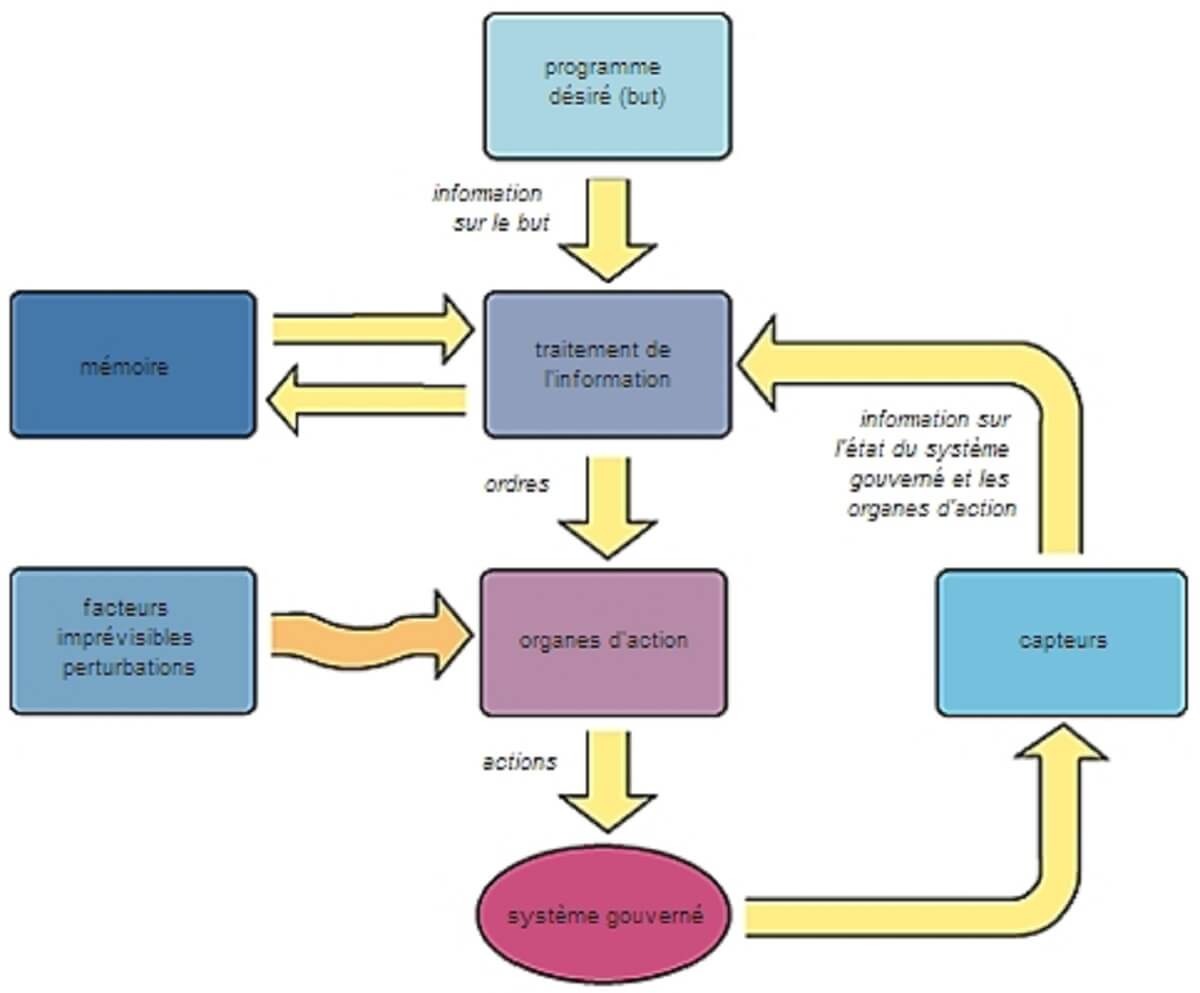
La cybernétique, c’est-à-dire, selon Wiener, la théorie de « la communication et de la commande chez l’animal et dans la machine », était née, mode d’étude de toute structure complexe organisée.
Dès sa publication en 1948, le livre Cybernetics eut un succès considérable et les idées de son auteur se répandirent très rapidement.
Pendant ses dernières années, Wiener publia de nombreux articles et volumes, seul ou en collaboration, sur la neurocybernétique et sur les implications philosophiques de la cybernétique.
Il s’est toujours élevé contre les déclarations excessives de certains inconditionnels en insistant sur le fait qu’en aucun cas une machine ne saurait se substituer au pouvoir de décision de l’être humain dont la responsabilité reste entière : « … en sorcellerie, on doit toujours demander ce qu’on veut vraiment et non quelque chose qu’on semble vouloir.
C’est la même chose avec l’automatisme moderne ; il est très facile de demander ce qu’on pense vouloir et qu’on ne veut pas. C’est un danger réel, spécialement de nos jours, quand il y a la possibilité d’employer les machines qui apprennent, qui jouent le jeu de la guerre, pour contrôler quand on doit pousser le bo […]









![[Chroniques – Voltaire avait raison] : « Le journalisme est le métier le plus difficile du monde, car il s’agit d’écrire l’Histoire au quotidien » La haine des juifs au temps des Lumières : le cas Voltaire ...](https://x7a7w8w2.rocketcdn.me/wp-content/uploads/2019/09/La-haine-des-juifs-au-temps-des-Lumières-le-cas-Voltaire-...-324x235-1.jpg)





